漸化式（Δr）の解説（詳細）

用語の整理

a, b, c, ωなど、計算時に値に置き換わる物　⇒　変数
＋、×、Σなど、変数同士を繋ぐ物　⇒　計算記号

演算と効果

数式には様々な計算記号(+、-、×、÷、等)が使わるが、使われ方によって効果の大きさが大きく異なる。
基礎的な話や厳密な話は数学の教科書を読んで貰うとして、以下にこのゲームで活用できる要素を紹介しよう。

　1. 計算記号の違いによる傾向の違い

このゲームは、様々なアップデートで変数の値や変数自体を増やしくのだが、
その変数同士を繋ぐ計算記号によって、計算結果の値の大きさが異なってくる。

	足し算（＋）	かけ算（×）	べき乗（^）
0.1	0.1 + 0.1 = 0.2	0.1 × 0.1 = 0.01	0.1 ^ 0.1 = 0.794...
1	1 + 1 = 2	1 × 1 = 1	1 ^ 1 = 1
2	2 + 2 = 4	2 × 2 = 4	2 ^ 2 = 4
5	5 + 5 = 10	5 × 5 = 25	5 ^ 5 = 3125

特徴は以下の通り。

　足し算：計算結果のほうが常に大きくなるが、増え幅は小さい。
　かけ算：1を下回ると計算結果の方が小さくなる。値が大きくなると増え幅が大きい。
　べき乗：値が大きくなるとかけ算よりも増え幅が大きい。

このゲームのアップグレードの半分以上は、変数に数値が足される形となる。
なので、かけ算やべき乗に絡む変数を強化した方が、結果として大きな値になっていく事になる。

ちなみに、「+n％」という強化は「×(1+n÷100)」という計算。
隠れたかけ算の強化なので、覚えておこう。

　2. 数値の大小関係による効果の違い

このゲームの中心にある数式が「A=a×b×c×d×e×f×g」というもの。
ゲームをやり始めて少し経つと、「aの強化よりe,f,gの強化の方が効果がある」と感じるだろう。

Rアップグレードの基本は、a～gの数値自体を足し算で増加させていくものだが、
値のバラツキ方によって、同じ＋1でも計算結果への影響が大きく異なる。

例1：a=4, b=4, c=4, d=4, e=4, f=4, g=4の場合
　　4×4×4×4×4×4×4＝16,384
　　　gを+1増加させると
　　4×4×4×4×4×4×5＝20,480 (+25%)

例2：a=7, b=6, c=5, d=4, e=3, f=2, g=1の場合
　　7×6×5×4×3×2×1＝5,040
　　　gを+1増加させると
　　7×6×5×4×3×2×2＝10,080 (+100%)

これから分かることは、計算記号が同じ場合、変数の値が小さい物を強化した方が効果が大きい、ということ。
ただし、現実には強化に必要なコストが異なるため、費用対効果(コスト対効果)で見るとこうなるとは限らない。
もし選べるならば、という位で考えておこう。

ちなみに、「ストアの変数ブーストはb～gのどれから買った方が良いか」と疑問に思う人も居るかも知れないが、
b～gのどれを強化してもAの値自体は変わらない。
どこもかけ算同士のため、式変形をするとどれも変わらないことが分かる。
※ただし、Rアップグレード11番目の都合により、
最終数値としては値の大きい変数にブーストをした方が効果が大きくなる。

---

数式解説

①初期段階（転生するまで）

足し算、かけ算、べき乗だけで構成されている。

変数	解説
ω	ω転生によって数値が増え、べき乗の値も増えていき、a～gの全てとかけ算で繋がっている。 数値に大きな影響を与える変数だということがわかるだろう。
k	kだけは他の変数とは分かれた所で、最終的に加算されるだけになっている。 いくらkを強化しても、通常はAなどと比べると小さな値にしかならないので、 これだけだと効果が薄いと分かる。

②転生後

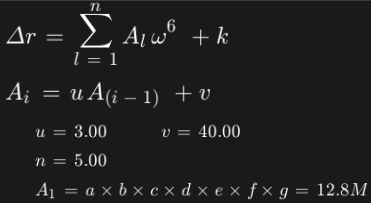
Σが現れ、数列の和を求める漸化式そのものとなる。

1つ目の式は「数列A_lをl=1から順にl=nになるまで足して、ω⁶をかけ、kを足す」ことを意味する。
ここではn=5なのでΔr=[ω⁶×（A₁+A₂+A₃+A₄+A₅）]+k

2つ目の式は「数列A_lにおいて、A_iはA_i-1にuをかけ、vを足した数である」ことを意味する。
例えば　A₂ ＝ u × A₁ + v = 3 × 1280000 + 40 = 3840040

変数	解説
n	足し算の部分をいつまで繰り返すか示す値 nが大きいほど、この漸化式は値が大きくなっていく (Aが正の数であることが前提)
u	一見すると単に「u×A」としているだけに見えるが、 A1が大きな数字であり、A1の値に比べてvがかなり小さいので、A2はA1にuをかけた数とほぼ同じ。 つまり、「項(n)が増えるごとに繰り返しuをかけた値」になり、A1にun-1をかけた数とほぼ一緒になる。
v	①初期段階におけるkと似た感じ kと違って、vは強化する方法がかなり限られており、ほぼ影響を与えない

③T-13達成後

変数	解説
m	更に外側に追加されたΣの足し算の部分をいつまで繰り返すか示す値。 つまり②転生後の式がm回繰り返される。 ただし、この変数mを強化する方法はT-19にならないと解放されず、 それまでは約2倍止まりとなる。

④T-21達成後

A_iの式が定積分になる。

変数	解説
α β	βは「アップグレードの仕方を間違うとマイナス影響が出る」ものになっている。 このサイトで、問題の積分部分のグラフが見れる。 左側のスライダーでαの値を弄ると、それに伴ってグラフが変動する。 グラフは、x軸(横方向)がβの値、y軸(縦方向)が計算結果の大きさ。 初期状態のα=1.2のグラフを見ると、x軸が進むにつれてyが1に張り付き、 かなりβを高めないとプラスにならないことが分かる。 αを最低でも1.65以上まで強化してからβを強化し始めるのが1つの目安。